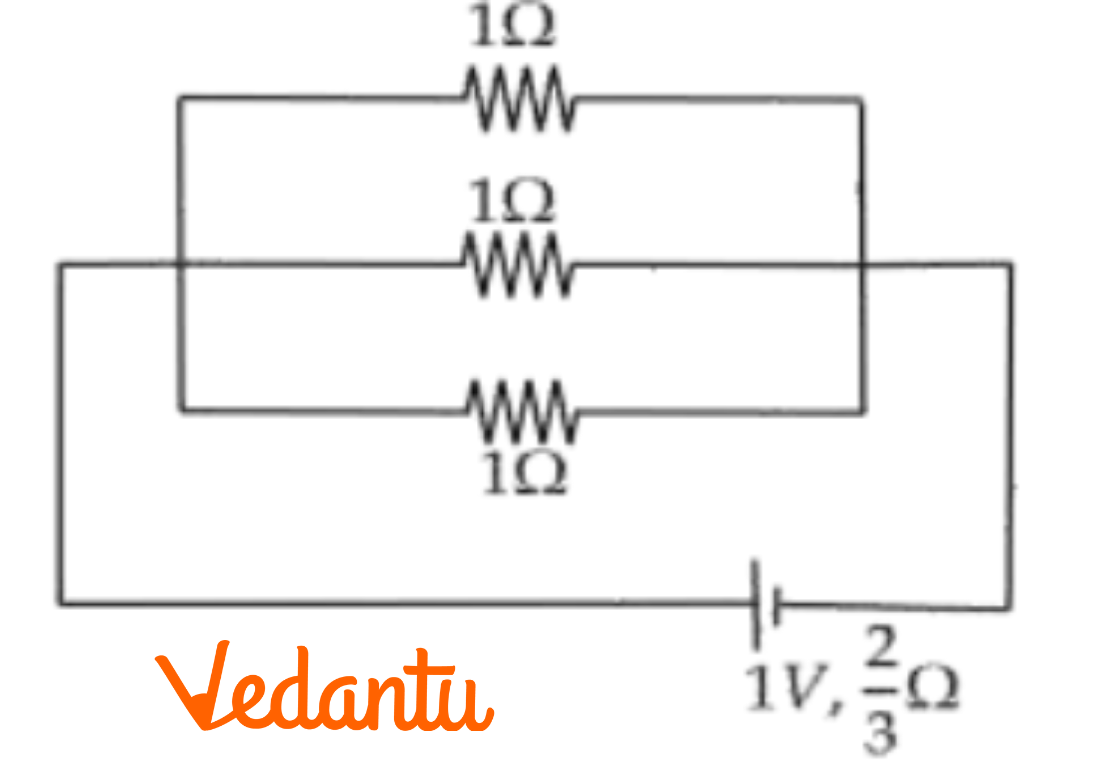
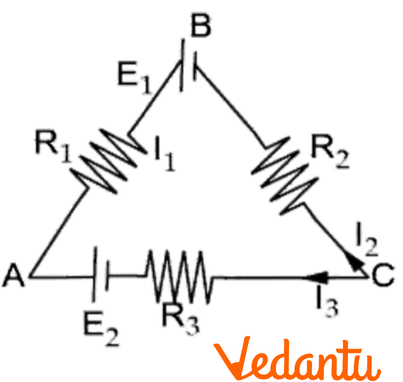
Download Important Questions for Class 12 Current Electricity FREE PDF



FAQs on Current Electricity Class 12 Important Questions: CBSE Physics Chapter 3
1. Which topics from Chapter 3, Current Electricity, are most important for the CBSE Class 12 Physics board exam in 2025-26?
For the Class 12 Physics board exam, the most frequently tested topics from Current Electricity that students must focus on are:
- Kirchhoff’s Laws: Both the junction rule (KCL) and the loop rule (KVL) are crucial. Expect direct numerical problems on complex circuits, often for 3 or 5 marks.
- Potentiometer: Its principle, and applications like comparing EMFs of two cells and finding the internal resistance of a cell, are very important. Derivations and circuit diagrams are frequently asked.
- Wheatstone Bridge and Meter Bridge: Understand the principle of a balanced bridge. Numerical problems to find an unknown resistance are common.
- Drift Velocity and its Relation to Current: The derivation of I = nAevd is a standard 2 or 3-mark question.
- Combination of Resistors and Cells: Problems involving series and parallel combinations, especially for cells (EMF, internal resistance), are important for numericals.
2. What is Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL)? Why are they considered so important for solving circuits?
Kirchhoff's laws are fundamental for analysing electrical circuits where Ohm's law alone is insufficient.
- Kirchhoff’s Current Law (KCL) or Junction Rule: It states that the algebraic sum of electric currents at any junction in a circuit is zero (ΣI = 0). This law is based on the conservation of charge.
- Kirchhoff’s Voltage Law (KVL) or Loop Rule: It states that the algebraic sum of all potential differences (including EMFs and voltage drops across resistors) around any closed loop in a circuit is zero (ΣV = 0). This law is based on the conservation of energy.
They are crucial because they allow us to systematically solve for unknown currents and voltages in complex, multi-loop circuits, which is a guaranteed type of question in board exams.
3. Explain the working principle of a potentiometer. Why is it preferred over a voltmeter for measuring the EMF of a cell?
A potentiometer works on the principle that when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length (V ∝ l).
A potentiometer is preferred over a voltmeter for measuring the EMF of a cell because:
- A potentiometer measures the EMF using a null deflection method. At the balance point, it draws no current from the cell whose EMF is being measured.
- The true EMF of a cell is its terminal potential difference when no current is drawn from it. Since the potentiometer meets this condition, it gives a highly accurate measurement of the EMF.
- A voltmeter, on the other hand, must draw some current from the circuit to show a reading, which causes a potential drop across the cell's internal resistance. Therefore, a voltmeter measures the terminal voltage (V = E - Ir), not the actual EMF (E).
4. A wire is stretched to double its original length. What is the effect on its resistance and resistivity? This is a common conceptual question in exams.
This is a classic higher-order thinking (HOTS) question. Here’s the breakdown:
- Resistance: When a wire is stretched to double its length (L' = 2L), its volume (V = A × L) remains constant. To compensate for the increased length, its cross-sectional area (A) must decrease. Since volume is constant, A'L' = AL, which gives A'(2L) = AL, so A' = A/2. The new resistance R' is given by R' = ρ(L'/A') = ρ(2L / (A/2)) = 4(ρL/A) = 4R. Therefore, the resistance becomes four times the original resistance.
- Resistivity (ρ): Resistivity is an intrinsic property of the material itself. It depends only on the nature of the material and its temperature, not on its physical dimensions like length or area. Therefore, when the wire is stretched, its resistivity remains unchanged.
5. What is a balanced Wheatstone bridge? For how many marks is a numerical based on it typically asked?
A Wheatstone bridge is an arrangement of four resistors in a quadrilateral shape, used to determine an unknown resistance. The bridge is said to be balanced when the potential difference between the two points of the galvanometer arm is zero, meaning no current flows through the galvanometer.
The condition for a balanced Wheatstone bridge is:
P/Q = R/S
where P, Q, R, and S are the resistances in the four arms of the bridge. Numerical problems based on this principle, including meter bridge applications, are very common and are typically asked for 2 or 3 marks in the CBSE board exam.
6. How does the resistance of a conductor and a semiconductor change with an increase in temperature? Explain why.
The temperature dependence of resistance is different for conductors and semiconductors, which is an important concept for exams.
- Conductors (Metals): For conductors, resistance increases with an increase in temperature. This is because as temperature rises, the thermal vibrations of the metal ions (kernels) increase. This leads to more frequent collisions between the free electrons and the ions, which decreases the average relaxation time (τ). Since resistance is inversely proportional to relaxation time (R ∝ 1/τ), the resistance increases.
- Semiconductors: For semiconductors, resistance decreases with an increase in temperature. This is because as temperature rises, more electron-hole pairs are generated due to the breaking of covalent bonds. This significantly increases the number density (n) of charge carriers. Although collisions also increase, the effect of the increased number density of charge carriers is much more dominant. Since resistance is inversely proportional to the number density (R ∝ 1/n), the resistance decreases.
7. State and derive the relationship between electric current and drift velocity of electrons. How is this derivation important for exams?
The relationship between electric current (I) and drift velocity (vd) is a fundamental derivation often asked for 2 or 3 marks. The relation is: I = nAevd
Derivation:
Consider a conductor of length L and uniform cross-sectional area A. Let 'n' be the number density of free electrons (number of free electrons per unit volume).
- The total number of free electrons in the conductor is N = (n) × (Volume) = nAL.
- The total charge on these free electrons is Q = N × e = nALe, where 'e' is the charge on one electron.
- The time 't' taken by an electron to travel the length L of the conductor with drift velocity vd is t = L/vd.
- By definition, electric current I is the rate of flow of charge, so I = Q/t.
- Substituting the values of Q and t, we get: I = (nALe) / (L/vd)
- Therefore, I = nAevd. This is the required relation.
8. What is the difference between the EMF of a cell and its terminal potential difference? When are these two quantities equal?
The distinction between EMF and terminal potential difference is a crucial concept for understanding cell circuits.
- EMF (E): Electromotive force is the maximum potential difference between the two terminals of a cell when it is in an open circuit (i.e., when no current is being drawn from it). It represents the total energy supplied by the cell per unit charge.
- Terminal Potential Difference (V): It is the potential difference between the two terminals of a cell when it is in a closed circuit (i.e., when current is being drawn from it). Due to the cell's internal resistance (r), some energy is lost as heat inside the cell. The relationship is given by V = E - Ir, where I is the current.
The EMF (E) and terminal potential difference (V) are equal only when the current (I) drawn from the cell is zero. This happens in an open circuit or when a potentiometer is used to measure the EMF at its balance point.
9. Why are alloys like Manganin and Constantan used for making standard resistance coils and in instruments like the meter bridge?
Alloys such as Manganin and Constantan are preferred for making standard resistors and wires for instruments like meter bridges and potentiometers due to two key properties:
- High Resistivity: They have a much higher resistivity compared to their constituent metals (like copper or manganese). This allows for a required resistance value to be achieved with a shorter, more manageable length of wire.
- Low Temperature Coefficient of Resistance: Their resistance does not change significantly with changes in temperature. This is extremely important for experimental setups where consistent resistance values are needed for accurate measurements, as the flow of current can cause heating (Joule heating).
10. What is an effective strategy for solving complex circuit problems using Kirchhoff's laws in the board exam to avoid errors?
Solving Kirchhoff's law problems requires a systematic approach to avoid sign convention errors and ensure full marks. For the 2025-26 board exam, follow this strategy:
- Step 1: Draw a Clear Diagram: Redraw the circuit if necessary and clearly mark all resistors, EMFs, and junctions.
- Step 2: Assign Current Directions: Assume a direction for the current in each branch. Don't worry if the assumption is wrong; the final answer will simply be negative, indicating the actual direction is opposite. Clearly label them (I₁, I₂, I₃, etc.).
- Step 3: Apply KCL (Junction Rule): Apply the junction rule to one or more junctions to get relations between the currents (e.g., I₁ = I₂ + I₃).
- Step 4: Apply KVL (Loop Rule) and Follow a Consistent Sign Convention: Choose independent loops and traverse them in a single direction (clockwise or anti-clockwise). Stick to a fixed sign convention:
- For EMFs: If you move from the negative to the positive terminal, the EMF is positive. If you move from positive to negative, it is negative.
- For Resistors: If you move in the same direction as the assumed current, the potential drop (IR) is negative. If you move opposite to the current, it is positive.
- Step 5: Solve the Equations: You will have a set of simultaneous linear equations. Solve them carefully to find the values of the unknown currents.